[논문리뷰] An adaptive approach for determining batch sizes using the hidden Markov model-3

공부

[논문리뷰] An adaptive approach for determining batch sizes using the hidden Markov model-3

김지똥 2025. 3. 24. 01:16

이어서 진행해보자면,

다음 내용은

실험 시뮬레이션 및 결과 분석 (Simulation and Experimental Results)

논문에서는 HMM을 기반으로 배치 크기를 최적화하는 모델을 검증하기 위해 시뮬레이션 실험을 수행했다.
➡ 실험에서는 산업 로봇(MH, Material Handler)과 CNC 가공 기계(MP, Machining Processor)가 있는 제조 시스템을 고려하여 배치 크기를 결정하는 방식을 테스트했다.

실험 시스템 설명 (System Description)

시스템 개요

산업 로봇 (MH, Material Handler):
- 부품을 픽업하고, 가공 기계(CNC 머신)로 이동시킨다.
- 제품의 위치(Location)에만 영향을 미친다 (정확한 위치에 놓여야 함).
CNC 가공 기계 (MP, Machining Processor):
- 부품을 절삭 가공한다.
- 제품의 치수(Dimensional Tolerance) 및 위치(Location Tolerance)에 영향을 미친다.

실험 목표

배치 크기 결정 모델이 실질적으로 제조 공정에서 어떻게 적용될 수 있는지 검증하기 위함이다.
공정 변동성(Variability)이 증가할 경우, HMM을 통해 이를 감지하고 배치 크기를 적응적으로 조정하는지 확인한다.

실험 과정

로봇(MH)이 부품을 집어 CNC 가공 기계(MP)로 이동시킨다.
CNC 가공 기계가 부품을 가공한다.
가공된 부품의 품질 데이터를 수집하여, HMM을 통해 공정 상태를 예측한다.
다음 배치 크기를 결정한다(배치 크기를 늘리거나 줄일지 판단).

➡ 즉, 로봇이 배치를 이동시키고, CNC 가공이 완료되면 품질 데이터를 분석하여 배치 크기를 조정하는 방식이다.

시스템에서 사용된 변수 및 데이터 구조

각 장비가 제품 품질에 미치는 영향

로봇(MH)의 영향:
- 제품의 위치(Location) 정확도에 영향을 미친다.
- 만약 위치 오차가 커지면, 가공 정밀도도 영향을 받을 수 있다.
CNC 기계(MP)의 영향:
- 제품의 치수(Dimension) 및 위치(Location) 정확도에 영향을 미친다.
- 기계의 성능이 저하되면, 제품의 품질 편차가 증가한다.

품질 데이터 변수 정의

제품 i의 관측 데이터 Oi. Oi=(Oi,1,Oi,2,...,Oi,F)
- 제품이 가공된 후 측정된 품질 데이터 (치수 및 위치 편차 포함).
- F는 제품의 품질 특성(예: 치수, 위치 등)의 개수.
상태 변수 (HMM에서 학습할 상태값)
- 로봇(MH)과 가공기(MP)의 상태를 각각 정의한다.

데이터 생성 과정

제품의 품질 데이터는 정규 분포(Gaussian Distribution)를 따르는 것으로 가정된다.
HMM 모델을 적용하여, 시간이 지남에 따라 상태가 변화하는 과정을 반영한다.

실험 데이터 생성 과정 (Algorithm 1 - Generating Data Set)

실험 데이터 생성 목적

공정 변동성(Variability)이 랜덤하게 발생하도록 시뮬레이션하여, HMM이 이를 제대로 감지할 수 있는지 확인하는 것이 목적이다.
변동성은 포아송 분포(Poisson Process)를 이용하여 랜덤하게 발생하도록 설정된다.

데이터 생성 과정 요약 (Algorithm 1)

초기 설정:

input:

L : 공정 길이 (총 생성할 품질 데이터 수, 예: 500개 부품)

F : 제품의 품질 특성 수 (예: 위치, 치수 등)

C : 공정에 포함된 장비 개수

Θ₀ : 초기 품질 분포 파라미터 (정상 상태에서 시작함)

T^L, T^D± : 각각 위치/치수 허용 오차 (공차 tolerance)

i : 현재 공정의 위치 (i번째 부품)

p : 지금까지 발생한 이상(abnormality)의 횟수

RNₚ : 포아송 분포 기반으로 생성된 다음 이상 발생 시점 리스트

output :

: 제품 1번부터 L번까지의 품질 데이터의 나열

 Set i = 0, p = 1

i : 현재까지 처리한 제품 수

p : 발생한 이상 패턴 수

Initialize Θ₀

: 공정은 초기 상태로 시작 (정상 상태)

Generate random numbers corresponds to Poisson process

: 포아송 분포에 따라 공정 이상이 발생하는 시점을 RNₚ 배열에 저장
(예: RNₚ = [140, 220, 400] → 140번째, 220번째, 400번째 부품 이후 공정 상태가 바뀜)

while 루프 (i ≤ L)

💡Case 1: 아직 다음 이상 발생 시점 전 (i < RNₚ)

if p == 1:
    generate observation

: 초기 상태, 아직 이상 패턴 없음 → 그냥 품질 데이터를 현재 파라미터 Θ로 생성.

else:
    update value of parameters
    generate observation

이상 패턴이 한 번 이상 발생한 경우
현재 파라미터를 비정상 상태로 업데이트 (예: 분산 증가, 평균 편향 등)
해당 상태로 관측 데이터 생성

💡Case 2: 새로운 이상 발생 시점에 도달 (i ≥ RNₚ)

select abnormal patterns, equipment, parameters...
update value of parameters
generate observation
set p ← p + 1

새로운 이상 발생
무작위로 어떤 장비에 어떤 이상이 발생할지 결정함
예: MP의 위치 분산 증가, MH의 위치 편차 발생 등
이를 기반으로 파라미터 업데이트
해당 상태에서 관측값 생성
이상 발생 횟수 p를 1 증가시킴

결과적으로,

L개의 제품에 대한 품질 데이터 {O_i}을 생성했다.

이 데이터는 시간이 지날수록 공정의 변동성, 이상 발생을 반영한다.

HMM 학습 및 배치 크기 최적화 테스트에 사용할 수 있다.

➡ 즉, 공정 변동성이 발생하는 환경을 가정하고, 이를 기반으로 배치 크기를 조정하는 실험 데이터를 생성하는 과정이다

최종 정리 – 실험에서 검증한 사항

실험 환경

산업 로봇(MH)과 CNC 가공기(MP)가 있는 제조 시스템을 가정함.
제품이 생산되면서 품질 데이터를 수집하고, HMM을 통해 공정 상태를 예측함.
변동성이 발생하면 배치 크기를 조정하여 품질을 유지하는 것이 목표.

HMM을 활용한 공정 모니터링

제품 품질 데이터를 통해 공정 상태(정상 vs. 비정상)를 실시간으로 감지함.
변동성이 감지되면 배치 크기를 줄여 불량률을 최소화함.

실험 데이터 생성 방법

공정 변동성이 포아송 분포를 따르도록 설정하여 현실적인 시뮬레이션을 수행함.
데이터는 정규 분포를 기반으로 생성되며, 공정 변동성이 커지면 품질 편차가 증가하도록 설정됨.

결과 분석을 위한 데이터 구조

로봇과 가공기의 품질 영향을 따로 분석할 수 있도록 변수 설정
위치 오차(Location Tolerance)와 치수 오차(Dimensional Tolerance)를 각각 분석

➡ 이 실험을 통해 HMM이 제조 공정에서 배치 크기를 조정하는 데 효과적으로 사용될 수 있음을 확인하려는 것이다.

실험 결과 분석 (Experimental Results) – HMM 기반 배치 크기 결정 모델 성능 검증

논문에서는 HMM 기반 배치 크기 조정 모델을 검증하기 위해 3000개의 시뮬레이션 데이터를 생성하고 실험을 진행했다.
➡ 기존 방식(PDP 기반 모델)과 비교하면서, HMM 모델이 배치 크기를 조정하는 능력이 얼마나 효과적인지 분석한다.

실험 개요

목적:

HMM 모델이 실시간으로 품질 데이터를 분석하여 배치 크기를 효과적으로 조정할 수 있는지 확인한다.
전통적인 PDP 모델(Predefined Defective Probability Model)과 비교하여 성능 차이를 분석한다.

실험 방식:

3000개의 공정 데이터를 생성하여 HMM 모델을 학습한다.
새로운 3000개의 배치 데이터를 테스트하여 성능 평가한다.
EM 알고리즘을 사용하여 매 500배치마다 모델 업데이트 진행한다.
다음 배치 크기 결정 시, 품질 데이터 기반으로 공정 상태를 예측하여 크기 조정한다.
기존 PDP 모델과 비교하여 불량률(Defective Rate)과 배치 크기(Batch Size) 비교한다

주요 실험 결과 분석

Fig. 6 – 배치 크기와 불량률 비교 (Proposed Model vs. PDP Model)

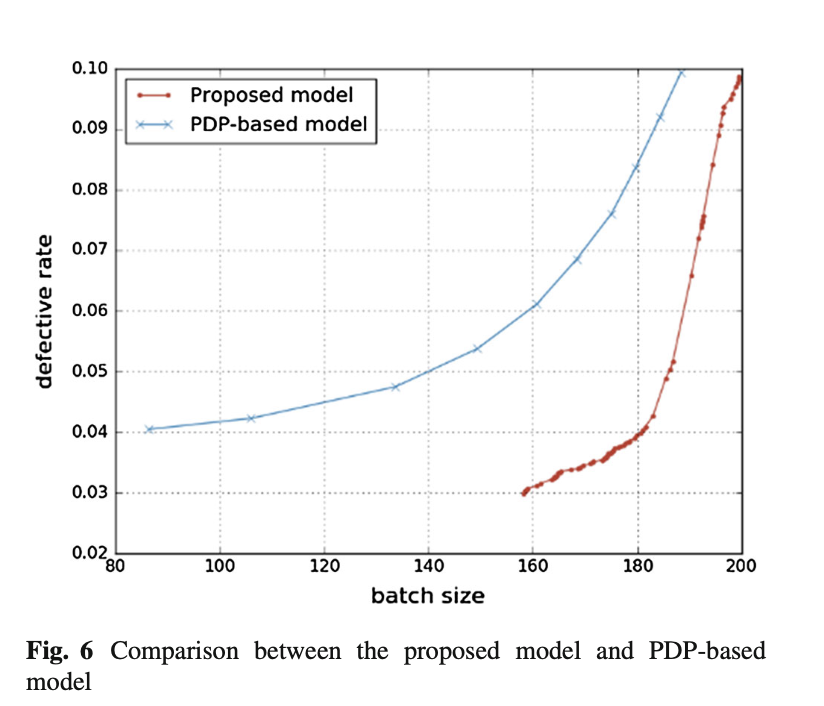
배치 크기(Batch Size) vs. 불량률(Defective Rate) 그래프
Proposed Model (HMM 기반)은 더 큰 배치 크기를 유지하면서도 낮은 불량률을 기록했다.
PDP 기반 모델은 배치 크기가 작고, 불량률이 상대적으로 높다.

의미:
➡ HMM 기반 모델은 품질 변동성을 실시간으로 예측하여, 불량률이 낮은 상태에서 배치 크기를 증가시킬 수 있다.
➡ PDP 모델은 사전에 정해진 불량률 기준을 유지하기 위해 배치 크기를 제한하는 방식이라 최적화가 부족하다.

Table 1 – 수치 비교 (Batch Size & Defective Rate)

HMM 모델은 허용 불량률(δ 값)이 증가할수록 배치 크기를 크게 조정할 수 있다.
HMM 모델은 기존 PDP 모델보다 배치 크기가 크면서도, 불량률이 더 낮다.
PDP 모델은 불량률이 0.05 이상 증가하면서도 배치 크기가 작다.

의미:
➡ HMM 기반 배치 크기 조정 모델이 더 높은 효율성을 제공하며, 불량률을 낮추는 데 효과적이다.

Fig. 7 – Fast Stop (빠른 정지 기능)

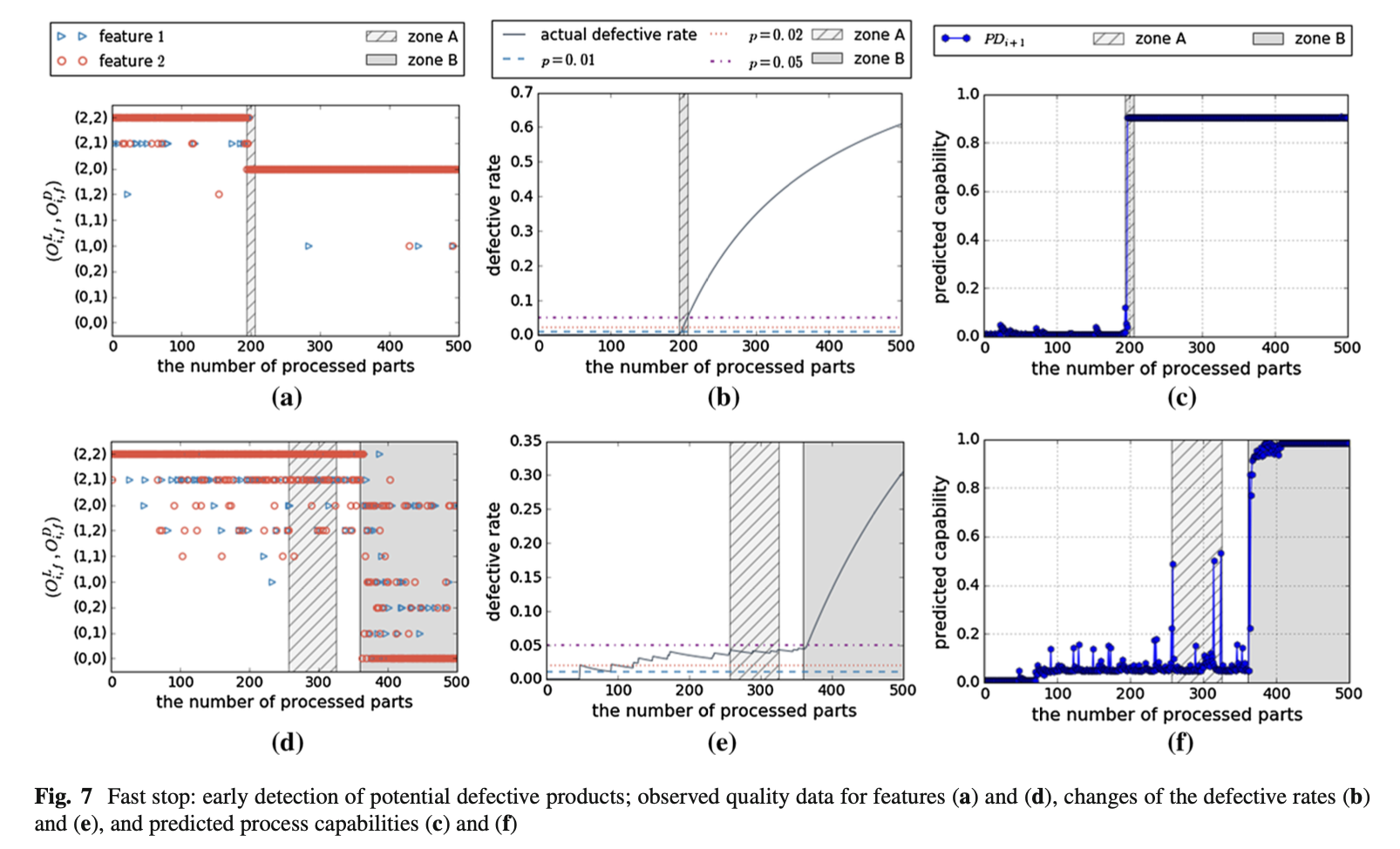
"Fast Stop"이란?

HMM 모델이 공정 품질이 나빠질 것으로 예상되면 즉시 배치를 종료하고 재조정하는 기능이다.
Fig. 7에서 Zone A에 들어서기 직전 HMM 모델(a-c)이 배치를 종료한다.
PDP 모델(d-f)은 불량률이 0.05를 넘을 때까지 계속 생산하다가 늦게 조정한다.

의미:
➡ HMM 기반 모델은 불량률이 올라가기 전에 사전에 감지하여 배치를 종료하는 "Fast Stop" 기능을 수행할 수 있다.
➡ PDP 모델은 불량률이 0.05를 초과한 후에야 배치 크기를 조정하므로 반응 속도가 늦다.

Fig. 8 – Robustness (강건성, 견고함)

HMM(a-c) 모델은 공정 상태가 좋은 경우 배치 크기를 증가시킬 수 있음.
Zone A에서는 일부 불량이 발생했지만, Zone B에서 품질이 회복되면서 배치 크기가 증가함.
PDP 모델(d-f)은 고정된 배치 크기를 유지해야 하므로 품질이 좋아져도 배치 크기를 증가시키지 못함.

의미:
➡ HMM은 약간의 불량으로는 공정을 멈추지 않음, 불량이 나오더라도 공정 상태가 좋으면 계속 가동.
➡PDP는 불량이 발생한 후 대응, 사후 대응 -> 최적화에 한계가 있음.

최종 결론 – HMM 기반 배치 크기 조정 모델의 장점

1. 더 큰 배치 크기 유지 가능

HMM 모델은 불량률을 낮추면서도 배치 크기를 최적화할 수 있음.생상성 향상!

2. 불량률을 사전 예측하여 빠르게 조정 가능 (Fast Stop)

HMM 모델은 불량률이 증가할 것으로 예상되면 사전에 배치를 종료하여 품질을 유지함.
기존 PDP 모델은 기준 불량률을 초과한 후에야 조정이 가능하여 반응 속도가 늦음.

3. 공정 상태가 양호하면 배치 크기를 증가 가능 (Robustness)

HMM 모델은 공정 품질이 양호한 경우 배치 크기를 증가시켜 생산 효율을 극대화할 수 있음.
PDP 모델은 고정된 규칙에 의해 운영되므로 최적화할 수 없음.

4. 실시간 데이터 기반 최적화 가능

HMM 모델은 실시간으로 공정 데이터를 분석하여 최적의 배치 크기를 조정할 수 있음.
기존 PDP 모델은 사전에 설정된 규칙만 따르므로 유연성이 떨어짐.

결론 – HMM 기반 배치 크기 조정 모델이 효과적인 이유

불량률을 낮추면서도 배치 크기를 최적화할 수 있음.
"Fast Stop" 기능을 통해 사전 예측 및 배치 종료가 가능하여 불량을 최소화함.
"Robustness" 기능을 통해 공정 품질이 양호할 때 배치 크기를 증가시켜 생산성을 극대화할 수 있음.
실시간 데이터를 기반으로 공정을 최적화할 수 있음.

➡ HMM 기반 모델이 기존 PDP 모델보다 더 효과적인 배치 크기 조정 방안을 제공함을 실험적으로 입증한다.