고정 헤더 영역
상세 컨텐츠
본문
1.2 Optimization with Data Uncertainty
최적화 문제를 다룰 때 매개변수가 정해진 문제들도 있지만 사실은 그렇지 않은 경우가 더 많다.
특히 투자 수익률이나 위험, 금융 모델과 같은 변동성을 포함하는 문제에서 자주 발생한다.
따라서 이러한 문제를 다루기 위해 두 가지 접근법이 존재한다.
- 확률적 계획법(Stochastic Programming): 데이터의 불확실성이 확률 분포로 설명될 수 있고, 랜덤하게 발생하는 경우에 사용된다. 즉, 데이터가 확률적으로 어떤 분포를 따를 때 이를 모델링하는 방법이다. 이 방법은 불확실성이 랜덤하게 발생하며, 우리가 그 랜덤성을 통계적으로 알 수 있는 상황에서 적합하다. (Finance에 관한 내용이니까 앞으로 이것에 집중하여 이야기 하지 않을까 한다)
- 강건 최적화(Robust Optimization): 데이터가 어떤 불확실성을 가지고 있을지 모르지만, 그 불확실성이 모든 가능한 경우에 대해서도 최악의 상황을 대비하여 해결책이 좋은 성능을 보이도록 하고자 할 때 사용된다. 즉, 불확실한 데이터의 모든 실현 가능성에 대해 최적의 해를 찾는 방법이다.
두 방법의 비교
- 불확실성 모델링 방식:
- 확률적 계획법은 불확실성을 확률 분포로 모델링한다. 즉, 미래 데이터가 확률적으로 어떻게 분포할지 아는 경우에 사용한다.
- 강건 최적화는 불확실성을 범위로 다룬다. 확률 분포가 없는 경우, 가장 나쁜 상황을 고려해 해결책을 찾는다.
- 해결책의 성격:
- 확률적 계획법은 기대값을 최적화하는 방식이다. 여러 시나리오에서 평균적으로 좋은 결과를 기대하는 해결책을 찾는다.
- 강건 최적화는 최악의 상황을 대비한다. 데이터가 불확실할 때도 항상 성능이 보장되는 보수적인 해결책을 추구한다.
1.2.1 Stochastic Programming
위에서 설명했듯 확률적 계획법은 일부 문제의 데이터가 랜덤하게 변화할 때 사용하는 최적화 방법을 말한다.
확률적 계획법은 사후 결정(recourse actions)을 포함할 수 있다. 이는 일부 의사결정을 내린 후에, 랜덤한 사건의 결과를 관찰한 뒤 추가적인 의사결정을 내릴 수 있다는 것을 말한다. 예를 들어, 2단계 확률적 선형 계획 문제(two-stage stochastic linear program)는 다음과 같이 표현될 수 있다:

- 확률적 계획법은 랜덤한 데이터가 포함된 최적화 문제를 해결하는 방법이다.
- 2단계 확률적 계획법에서는 첫 번째 결정 이후에 랜덤 사건이 발생하고, 그 사건의 결과에 따라 두 번째 결정을 내린다.
- f(x)는 두 번째 단계의 최적화 문제의 기대값을 나타내며, 이를 최적화하는 것이 전체 문제의 목표다.
따라서 함수 의 특성에 따라 최적화 문제의 형태가 결정되며, 그에 맞는 알고리즘을 사용하여 문제를 쉽게 풀 수 있다.
1.2.2 Robust Optimization
위의 설명처럼 강건 최적화는 데이터 불확실성을 고려하여, 모든 가능한 불확실한 상황에서도 좋은 성과를 내는 해결책을 찾는 방법이다.
확률적 계획법(Stochastic Optimization)과는 달리, 모든 가능성을 동일하게 중요하게 생각하며, 불확실한 데이터가 어떻게 발생할지 몰라도 항상 일관된 성능을 유지하는 해를 찾는 것을 목표로 한다.
제약 강건성(Constraint Robustness)
강건 최적화의 중요한 개념 중 하나는 제약 강건성(Constraint Robustness)이다. 이 개념은 불확실한 입력 값들이 무엇이든 간에, 모든 가능성에 대해 문제의 해가 유효하게 유지되는지를 평가한다. 즉, 불확실한 데이터의 모든 값에 대해 제약 조건을 만족하는 해결책을 찾는 것이 목표이다.
예시)
Ben-Tal과 Nemirovski가 제시한 예시에서, 다단계 공학 프로세스(예: 화학 증류 공정)를 고려한다. 이 공정에서 각 단계로 들어가는 재료의 양이 외부 요인에 의해 변동할 수 있다. 불확실성이 있더라도 모든 단계의 균형 제약 조건을 만족해야 한다.
강건 최적화는 다음과 같은 문제로 표현될 수 있다.
(OPuc : Uncertain Constraints인 최적화 문제)
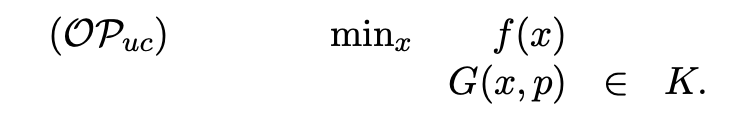
- : 결정 변수.
- : 확정적인 목적 함수.
- : 불확실한 매개변수 p에 따라 변화하는 제약 함수.
- : 구조적인 제약 요소.
- : 불확실한 매개변수.
불확실한 매개변수들이 속하는 집합 가 주어지면, 제약 강건한 해를 찾는 문제는 다음과 같이 표현된다.
(CROP는 Constraint Robust Optimization Problem의 약자로, 제약 강건 최적화 문제)

목표 강건성(Objective Robustness)
또 다른 중요한 개념은 목표 강건성(Objective Robustness)입니다. 이는 목적 함수에 불확실한 매개변수가 포함된 경우 발생한다. 목표 강건성은 불확실한 매개변수들의 모든 실현 가능한 값에 대해 해가 최적에 가까운 상태를 유지하는지 평가하는 개념이다.
이 개념을 수식으로 나타내면:
(는 Objective Uncertainty Optimization Problem의 약자로, 목적 함수가 불확실한 최적화 문제를 의미)
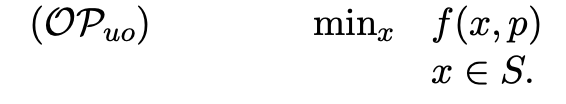
여기서, 는 유효한 해가 존재하는 집합이고, 는 불확실한 매개변수 p에 의존하는 목적 함수다.
이를 통해 모든 가능성에 대해 최악의 상황을 대비한 해를 찾는 것이 목적이다.
최종적으로, 목표 강건 해를 찾는 문제는 다음과 같이 표현된다:
(OROP는 Objective Robust Optimization Problem의 약자로, 목표 강건 최적화 문제)
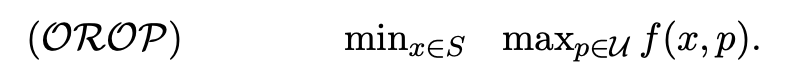
'공부 > 파이썬' 카테고리의 다른 글
| #13. 백준 2720번 (python) (0) | 2025.02.25 |
|---|---|
| #12. 백준 2164번 (python) (0) | 2025.02.06 |
| [파이썬] return과 print의 차이 (0) | 2024.08.26 |
| #11. 백준 11718번 (python) (0) | 2024.08.10 |
| #10. 백준 5622번 (python) (0) | 2024.08.07 |




