고정 헤더 영역
상세 컨텐츠
본문
요즘 진행하고 있는 프로젝트를 위해서 공부를 진행하고 있다.
그에 가장 관련 있는 논문에 대해 알아보고 혹시나 틀린 부분 있으면 피드백을 받기 위하여 글을 남긴다.
현대 FHMM에 대해 공부하고 있기에 그와 관련있는 HMM 관련 논문을 가져왔다.
(아무것도 모르는 아기라고 생각하시고 읽어주세요 ㅜㅜ. 틀려도 이해해주기!)

[Abstract]
논문에 대해 간단히 설명하자면
물건을 만드는 공장에서는 물건을 생산할 때 일정한 단위(Batch)로 생산한다.
타이어 공장을 예로 들어보자. 타이어를 만들기 위해선 원재료를 녹이는 과정이 필요하다. 이때 아래의 그림처럼 적은 분량의 원재료를 녹여 하나의 타이어를 만들고 또 하나 타이어 하나를 만들면 품질은 좋겠지만 시간과 비용이 엄청나게 소요된다.


그렇기 때문에 일정한 단위로 나누어 물건을 생산하는데 기존의 접근 방식은 배치 크기를 수학적으로 모델링하고, 특정 제약 조건(예: 비용 최소화, 품질 보장)을 설정하여 최적해를 찾는 방식이었다. 하지만 이러한 방법은 시스템의 변동성(variability)이 일정하다는 가정하에 작동하며, 현실에서는 적용이 어렵다.
이 논문에서는 최근 데이터 기반 프로세스 분석 기법을 활용하여 동적인 변동성을 고려한 배치 크기 결정 모델을 제안한다. 특히 Hidden Markov Model (HMM, 은닉 마코프 모델)을 사용하여 제품 품질 데이터를 분석하고, 재조정(recalibration)이 필요한 시점을 동적으로 예측하는 방법을 제시한다.
그러니까 이 연구는 배치 크기 결정 문제를 정적인 접근법에서 동적인 접근법으로 확장한 것이 핵심이다. 기존의 고정된 모델 대신, 실시간으로 변동성을 분석하고 최적의 배치 크기와 재조정 시점을 예측할 수 있는 새로운 방법을 제안했다. 이를 통해 제품 품질을 유지하면서도 효율적인 생산이 가능해진다.
그 다음은 정의에 대한 부분이다. 지도 교수님께서는 뭐든 시작 전 정의를 하고 다음 단계로 넘어가야한다고 말씀하셨다.
(어떻게 보면 당연한 말이지만 본인은 그러지 않았다. 문제에 들어가기 앞서 정의하는 습관을 기르자)


[Introduction]
제조 시스템에서 변동성의 영향
- 제조 시스템의 성능(품질, 기계 활용도 등)은 운영 과정에서 필연적으로 변동성을 포함한다.
- 변동성을 완전히 제거하는 것은 사실상 불가능하며, 변동성이 클수록 불량품 발생 확률이 증가하여 제조 비용이 상승한다.
- 시스템이 제어 상태(in-control state)에서 비제어 상태(out-of-control state)로 변화하는 과정은 지수분포(exponential distribution)를 따른다. 따라서, 공정 시간이 길어질수록 변동성이 증가하여 제품 품질이 저하될 가능성이 높다.
*제어 상태(in-control state) : 공정이 정상적으로 운영되는 상태 (예를 들어, 기계가 새것이나 최근 정비가 완료된 상태일 때..)
*비제어 상태(out-of-control state) : 공정이 이상 상태로 변하는 상태 (예를 들어, 기계 마모, 온도 변화, 공구의 손상 등으로 인해 공정이 원래의 기준을 벗어나 변동성이 커지는 상태)
보통 수명 주기 모델하면 일반적으로(본인이 생각에) 배스 정리(Bathtub Curve)를 많이 떠올린다. 그러나 본 논문에서는 지수 분포를 언급하였다. 배스 정리가 아닌 지수 분포를 언급한 이유는 "공정이 정상적으로 작동하는 지속 시간(즉, 제어 상태가 유지되는 시간)이 랜덤하게 변하고, 특정 평균을 따른다고 가정"했기 때문이다.
가정에 대해 살펴 보면
1. 할당 가능한 원인(assignable cause)이 발생하면 시스템이 비제어 상태가 된다.
2. 이 할당 가능한 원인의 발생은 랜덤하며, 포아송 과정(Poisson Process)으로 모델링할 수 있다.
3. 포아송 과정에서 이벤트 간 간격(=제어 상태 지속 시간)은 지수분포를 따른다.
4. 따라서 공정이 비제어 상태로 변하는 과정은 지수분포를 따른다고 가정할 수 있다.
➡ 즉, 논문에서는 지수분포를 이용해 "제어 상태가 유지되는 시간"을 확률적으로 모델링한 것!
*할당 가능한 원인(assignable cause) : 쉽게 설명해보면 "갑자기 품질이 나빠졌는데, 그 이유를 명확히 찾아낼 수 있으면 ‘할당 가능한 원인’이다!" 금형 온도가 지나치게 높아지거나, 전력 공급이 불안정해서 속도가 느려지는 이유가 바로 할당 가능한 원인이다.
반다로 할당 불가능한 원인은 미세한 진동이나 편차와 같이 매우 작고 항상 있는 변화이다. 특정한 이유를 말하기 어려운 공정 내. ㅏ연스러운 변화가 여기에 해당한다.
그렇다면 논문에서 지수분포를 사용한 이유는?
➡ 공정이 정상적으로 유지되는 시간(=제어 상태 지속 시간)이 랜덤하게 변하고, 포아송 과정을 따른다고 가정하면 지수분포가 자연스럽게 등장하기 때문인 거 같다.
✔ 하지만, 현실적인 제조 시스템에서는 배스 정리(Bathtub Curve)나 웨이블 분포 같은 모델이 더 적절할 수도 있다.
✔ 단순한 모델을 사용한 이유는 수학적으로 계산이 쉽고, 초기에 공정 변동성을 분석할 때 자주 사용되기 때문인 거 같다.
지수분포를 사용한 이유를 알았으니 그에 따른 예로와 함께 더욱 자세히 살펴보자!
[상황: 공장 기계의 고장]
- 어떤 공장에서 기계가 고장이 나기 전까지 평균적으로 50시간 동안 정상적으로 작동한다고 가정하자.
- 하지만 고장이 발생하는 시점은 정확히 예측할 수 없고, 무작위로 발생한다.
- 기계가 정상적으로 작동하는 시간(즉, 제어 상태에서 비제어 상태로 변하기까지의 시간)이 지수분포를 따른다고 가정한다.
지수분포 적용
- 지수분포의 평균 1/λ는 기계의 정상 작동 시간의 평균, 따라서 λ = 1/50 (즉, 평균적으로 50시간마다 한 번씩 고장 발생).
- 지수분포의 확률 밀도 함수는:

이를 시각화 하면,

- X축 (Time t, 시간): 기계가 정상적으로 작동한 시간 (단위: 시간).
- Y축 (Probability Density, 확률 밀도): 특정 시간 t에 기계가 고장날 확률 밀도.
지수 분포 적용 이유:
배스 정리(Bathtub Curve) vs. 지수분포(Exponential Distribution)
🛑배스 정리(Bathtub Curve)
- 수명 주기를 초기 → 정상 → 노후 3단계로 나누어 설명한다.
- 기계가 처음에는 초기 불량(고장률 높음), 이후 안정적인 기간(고장률 일정), 마지막에는 마모로 인해 고장률 증가한다.
🛑지수분포(Exponential Distribution)
- "안정적인 기간(Useful Life Phase)"에 초점을 맞춘 모델이다.
- 이 단계에서는 고장률이 일정하다고 가정하며, 고장이 발생하는 시간이 메모리리스(memoryless) 특성을 가진다.
➡ 즉, 논문에서는 제조 공정의 "안정적인 기간"을 대상으로 했기 때문에 지수분포를 선택한 것이다.
➡ 하지만, 기계의 전체 수명 주기를 고려한다면 웨이블(Weibull) 분포나 배스 정리가 더 적절할 수도 있다.
HMM에서 상태 전이와 관측값
HMM이 은닉 상태(hidden state)를 기반으로 공정 변동성을 예측한다.
HMM에서 어떤 요소들을 상태(state)로 보고, 무엇을 관측(observation)하는지 더 구체적으로 설명하면,
🛑 HMM에서의 상태(State)
- 공정이 정상 상태 (In-control)인지, 비정상 상태 (Out-of-control)인지
- 즉, 공정의 "숨겨진 상태(hidden state)"가 정상 상태에서 비정상 상태로 전이된다.
🛑 관측값(Observations)
- 제품 품질 데이터 (예: 크기 편차, 표면 거칠기 등)
- 장비 상태 데이터 (예: 온도 변화, 진동 패턴 등)
➡ 이 데이터를 기반으로 "현재 공정이 정상 상태인지, 곧 변동성이 커질 것인지"를 예측하고 배치 크기를 조정한다.
➡ 이 부분을 보충하면 HMM이 실제로 어떻게 적용되는지 더 직관적으로 전달할 수 있을 것 같다.
[Literature review]
1. 품질 관리에서 변동성(variability) 감지 방법
- 기존에는 Shewhart, EWMA, CUSUM과 같은 통계적 품질 관리 기법을 사용했음.
- 하지만, 이러한 방법들은 특정 패턴(예: 급격한 변화, 추세 변화)만 감지할 수 있음.
- 머신러닝 기법(ANN, ICA, SVM, 하이브리드 모델) 적용 사례도 점점 늘어나고 있음.
2. 배치 크기 결정 연구 (Batch Size Optimization)
- EOQ (Economic Order Quantity) 모델이 초기 연구로 등장.
- 이후 확장 모델(EPQ: Economic Production Quantity)이 도입되며 변동성과 결함률을 고려하기 시작.
- 하지만 기존 연구는 정적인(static) 배치 크기 결정 모델을 기반으로 하고 있어, 변동성이 클 때 적절하지 않음.
3. HMM의 활용 및 한계점
- HMM은 제조 공정에서 시계열 데이터 분석에 유용하며, 다양한 응용 사례가 있음.
- 하지만, 기존 연구들은 HMM을 배치 크기 결정에 직접적으로 활용하지 않았음.
- 따라서, 이 논문은 HMM을 통해 변동성을 실시간으로 반영하는 배치 크기 조정 모델을 제안함.
기존 품질 관리 방법과 HMM의 차이점
✔ 기존 통계적 품질 관리 기법 (Shewhart, EWMA, CUSUM)
- 특징: 품질 데이터의 "이상치(outlier)"를 감지하고, 특정 임계값을 초과하면 경보 발생
- 한계점: 미리 정의된 기준(Threshold)이 필요하며, 공정의 동적 변화에 대응하기 어려움
✔ 머신러닝 기반 접근법 (ANN, SVM, ICA 등)
- 특징: 데이터 패턴을 학습하여 이상 징후를 탐지
- 한계점: 학습 데이터 품질에 의존하며, 해석력이 부족할 수 있음
✔ HMM 기반 접근법
- 특징: 공정 상태를 은닉(hidden) 상태로 모델링하여 변화 패턴을 추론
- 장점: 공정 상태 변화를 확률적으로 모델링하여 실시간으로 배치 크기 조정 가능
➡ 즉, HMM을 사용하면 기존 통계적 기법이 감지하지 못하는 변화 패턴을 인식하고, 머신러닝보다 해석력이 뛰어난 장점이 있다.
그렇다면 장점으로 가득한 HMM에도 한계점이 존재할까?
HMM은 데이터 의존성이 높다.
- HMM의 정확도는 학습 데이터 품질에 따라 달라짐
- 데이터가 부족하거나 품질이 낮으면, 공정 상태를 잘못 추론할 가능성이 있음
HMM의 상태(State) 설정이 어렵다
- 공정 상태를 몇 개의 상태로 나눌 것인지 결정하는 것이 어려움
- 만약 상태 수를 너무 많이 설정하면 모델이 과적합(overfitting)될 수 있음
실시간 적용이 어려울 수 있다.
- HMM 기반 모델을 실시간으로 운영하려면 센서 데이터 및 연산 능력이 필요
- 기존 공장에서는 이러한 데이터 인프라가 부족할 수 있음
Fig. 1 (불량률 변화 그래프)
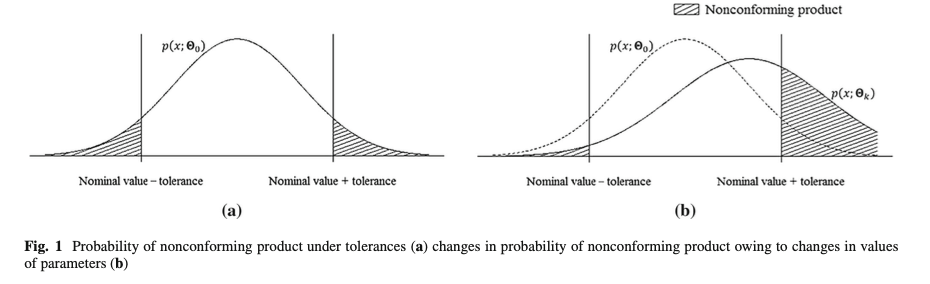
논문에서 제시한 Fig. 1은 제품의 불량률이 배치 변동성에 따라 어떻게 변하는지를 보여주는 그래프이다.
(a) 그래프: 변동성이 적을 때, 불량률이 낮다.
(b) 그래프: 변동성이 커질수록, 평균 값이 이동하며 불량률이 증가한다.
➡ 배치 크기 결정 시 변동성을 실시간으로 반영하지 않으면, 불량률이 증가할 수 있다는 점을 시각적으로 설명하는 그래프이다
➡ HMM을 이용하면 (b)와 같은 경우를 사전에 감지하여 배치 크기를 줄여 불량률을 낮출 수 있다.
[Process variability and product quality]
제조 공정 변동성(Process Variability)의 원인과 영향
제조 공정의 변동성 (Process Variability)이란?
- 제조 공정은 여러 요소(기계, 도구, 로봇, 작업자 등)로 구성되며, 이들 요소의 변동성(variability)이 제조 품질에 직접적인 영향을 미친다 (Western Electric Corporation, 1958; Kerzner, 2013).
- 공정 변동성의 대표적인 원인:
- 도구 마모(tool wear) → 시간이 지나면서 공구의 정밀도가 떨어짐
- 기계 설정 변경(machine configuration changes) → 온도, 진동 등의 환경 변화
- 모터 제어 정확도(motor control accuracy) 저하
- 기계 고장(machine breakdowns)
➡ 이러한 변동성이 누적되면서 제품 품질 저하로 이어질 수 있다 (Kuo & Mital, 1993).
변동성의 동적 변화 (Dynamic Variability)
- 공정이 진행될수록 도구의 마모가 증가하고, 기계의 성능이 달라지면서 변동성이 축적됨.
- 이 변동성이 일정한 것이 아니라, 시간이 지남에 따라 동적으로 변화하며, 그 결과 제품 품질이 점차 저하될 수 있음.
- 특히, 위치 편차(Positioning Deviation)와 같은 변동성은 장비의 상태나 환경 조건에 따라 예측하기 어려운 방식으로 변화함.
➡ 따라서 공정 변동성은 단순히 무작위적인 것이 아니라, 시간이 지나면서 누적되는 특성이 있다.
변동성이 제품 품질에 미치는 영향
제품 품질(Product Quality)의 평가 기준
- 제품 품질은 보통 특정한 확률적 분포(probabilistic distribution)로 표현됨.
- 제품의 품질 측정 예시:
- 치수 공차(Dimensional Tolerance) → 제품 크기가 설계된 규격 내에 있는지
- 위치 공차(Location Tolerance) → 부품의 위치가 원하는 좌표에 정확히 배치되었는지
➡ 즉, 제품의 품질은 각 부품의 측정값이 "설계 스펙(specification)"을 충족하는 정도에 따라 평가됨.
공정 변동성과 제품 불량률(Nonconforming Product Rate)
- 제품을 설계 규격과 비교했을 때, 허용 공차를 벗어나면 불량 제품이 됨.
- 공정 변동성이 커지면 치수 및 위치 편차가 커지고, 불량률도 증가함.
- Fig. 1의 그래프 해석:
- (a) 그림: 변동성이 적을 때, 불량률이 낮음
- (b) 그림: 변동성이 커질수록 평균 값이 이동하며 불량률이 증가
➡ 즉, 공정 변동성이 증가하면 제품이 설계 스펙을 벗어나 불량 제품이 증가할 가능성이 높아짐.
변동성 모델링 및 수학적 접근 (Mathematical Modeling of Variability)
논문에서는 변동성을 모델링하기 위해 확률 분포를 사용함.
위치 편차(Position Deviation)와 Rayleigh 분포 (Rayleigh Distribution)
- 실제 측정된 부품의 위치는 설계된 기준점에서 오차가 발생할 수 있음.
- 연구에 따르면, 위치 편차(Positioning Deviation)는 Rayleigh 분포를 따르는 것으로 알려짐 (Shapiro & Hahn, 1967).
- 즉, 실제 위치 오차의 크기(Deviation)는 Rayleigh 분포를 따른다는 가정.
치수 편차(Dimensional Deviation)와 정규 분포 (Normal Distribution)
- 치수 편차(예: 제품의 길이, 너비)는 보통 정규 분포(Normal Distribution)를 따름.
➡ 즉, 제품의 품질 요소(위치, 치수)는 서로 다른 확률 분포를 따르며, 이를 기반으로 불량률을 예측할 수 있음.
공정 변동성이 누적될 때 배치 크기 결정의 필요성
- 공정 변동성이 시간이 지나면서 누적되면, 점점 더 많은 제품이 설계 스펙을 벗어날 가능성이 높아짐.
- 하지만, 기존 연구에서는 배치 크기를 고정된 값으로 설정하여 이러한 변동성을 반영하지 못함.
- 따라서, 공정 변동성을 실시간으로 감지하여 배치 크기를 조정하는 모델이 필요함.
- 논문에서는 이를 HMM(Hidden Markov Model)을 이용하여 해결하는 방법을 제안함.
➡ 즉, 배치 크기를 "변동성을 고려하여 실시간으로 조정하는 것"이 핵심 아이디어이다.
예시를 통해 공정 변동성과 제품 품질의 관계에 대해 이해해보자.
반도체 제조 공정에서의 공정 변동성 (Semiconductor Manufacturing)
📍 반도체 공정에서 발생하는 변동성 요소
반도체는 나노미터(nm) 단위의 정밀한 패턴을 회로 기판에 새기는 작업이므로, 극도로 낮은 변동성이 요구된다. 하지만 다음과 같은 요인들 때문에 변동성이 발생할 수 있다.
✔ 포토리소그래피(Photo-lithography) 공정에서의 오차
- 반도체 회로를 새길 때 사용되는 광원이 미세하게 흔들리거나, 웨이퍼 표면의 반사율이 균일하지 않으면 패턴의 크기가 계획된 것과 다르게 나올 수 있다.
- 이로 인해 트랜지스터의 성능이 달라지고, 불량률이 증가할 가능성이 높아진다.
✔ 에칭(Etching) 공정에서의 도구 마모
- 웨이퍼를 가공하는 장비(플라즈마 장비 등)의 내부 부품이 시간이 지나면서 마모된다.
- 도구의 마모로 인해 웨이퍼 표면의 식각(etching) 속도가 균일하지 않게 되어 회로 품질이 저하된다.
- 초기에는 양품율(yield)이 높지만, 시간이 지날수록 변동성이 증가하면서 불량률이 올라간다.
➡ 결론:
반도체 제조에서는 공정 변동성이 시간이 지나면서 증가하며, 이를 실시간으로 감지하여 배치 크기를 조정하지 않으면 불량 반도체가 증가할 가능성이 높다.
📌 HMM을 활용하면?
- HMM을 적용하면 공정 상태(정상 vs. 비정상)를 실시간으로 추정 가능하고
- 변동성이 증가할 것으로 예측되면, 배치 크기를 줄여서 불량품 발생을 최소화할 수 있다.




