고정 헤더 영역
상세 컨텐츠
본문
KNN 거리 기반 분류 모델
데이터로부터 거리가 가장 가까운 k개의 다른 이웃 데이터의 레이블을 참조하여 분류하는 알고리즘
여기서 이웃 데이터들은 거리(distance)를 기반으로 판단
장점
- 간단하고 직관적인 알고리즘. 복잡한 수학적인 개념 없이도 이해하기 쉬움.
- 훈련 과정이 빠르며, 새로운 데이터가 들어올 때마다 다시 훈련할 필요가 없음.
- 분류와 회귀 문제에서 모두 사용할 수 있음.
- 이상치에 대한 영향을 크게 받지 않음.
단점
- 모든 데이터 포인트 간 거리를 계산해야 하므로, 계산 비용이 많이 들 수 있음. 특히 데이터가 많고 차원이 높을수록 더 많은 계산이 필요.
- 이웃의 수(k)를 어떻게 정할지에 따라 성능이 달라짐. 적절한 k값을 선택하는 것이 중요.
- 고차원 데이터에는 적합하지 않을 수 있음. 차원이 늘어남에 따라 공간의 크기가 지수적으로 커지기 때문에 거리 계산의 정확도가 떨어질 수 있음.
- 데이터의 분포에 따라 성능이 크게 달라질 수 있음. 데이터가 밀집되어 있지 않거나 균일하지 않으면 예측 성능이 저하될 수 있음.
x1 = np.arange(1,11)# 1부터 10까지의 숫자를 생성
x = x1.reshape(-1,1)#x1 배열을 2차원 배열로 재구성.
#-1은 해당 차원의 크기를 자동으로 계산하라는 의미이며, 1은 하나의 열(column)이 있음을 나타냄
y = np.arange(1,11)*5#1부터 10까지의 숫자를 생성한 후 각각에 5를 곱하여 y 배열을 생성KNN
knn_re=KNeighborsRegressor(n_neighbors=2).fit(x,y)KNeighborsRegressor 모델을 생성하고, n_neighbors 매개변수를 2로 설정하여 이웃의 수를 2로 지정한다. 그런 다음, fit() 메서드를 호출하여 모델을 입력 데이터 x와 대응하는 출력 데이터 y에 맞춘다.
KNN 알고리즘을 설정하는 데 사용되는 중요한 매개변수
- n_neighbors: 이웃의 수, 즉 k의 값입니다. 모델이 예측을 수행할 때 고려할 이웃의 개수를 나타낸다. 일반적으로 이 값은 홀수로 선택하여 두 가지 클래스를 구분할 수 있도록 한다.
- weights: 이웃의 가중치 결정 방법을 지정한다. 기본값은 'uniform'으로, 모든 이웃에 동일한 가중치를 부여한다. 'distance'로 설정하면 거리의 역수에 비례하여 가중치를 부여하므로, 더 가까운 이웃에 더 많은 영향을 받는다.
- metric: 거리 측정 방식을 지정한다. 대표적으로 'euclidean'과 'manhattan' 방식이 있습니다. 'euclidean'은 유클리드 거리를 사용하며, 'manhattan'은 맨하탄 거리를 사용한다.
- algorithm: 이웃을 찾는 데 사용할 알고리즘을 지정한다.
- 'auto': 알고리즘을 자동으로 선택한다. 주어진 데이터의 크기와 패턴에 따라 가장 적절한 알고리즘을 선택한다.
- 'ball_tree': 고차원 데이터에서 효율적으로 이웃을 찾기 위한 방법 중 하나이다.
- 'kd_tree': 데이터를 구조화하여 차원을 축소하면서 탐색하는 방법 중 하나이다.
- 'brute': 완전 탐색 방법으로, 모든 데이터 포인트를 비교하여 가장 가까운 이웃을 찾는다. 데이터가 많을수록 계산 비용이 증가한다.
이 매개변수들을 적절히 설정하여 KNN 모델을 조정하면, 모델의 성능을 향상시킬 수 있다.
KNN model 생성
난수 생성기에 동일한 시드를 성정하여 난수 생성 후 노이즈를 추가한다
그 후 n_neighbors = 5로 설절하여 모델을 만들고 시각화 하면

캘리포니아 주택가격 데이터셋을 사용하여 KNN을 회귀 모델로 훈련해보자
from sklearn.neighbors import KNeighborsRegressor
X,y = fetch_california_housing(return_X_y=True)#캘리포니아 주택가격 데이터셋 로드
데이터를 train,test로 나눈 후 다양한 k값에 대해 KNN 회귀 모델을 평가하여 최적의 k값을 찾기
for k in k_values:
knn = KNeighborsRegressor(n_neighbors=k)
scores = cross_val_score(knn, X_train, y_train, cv=3, scoring='neg_mean_squared_error')
mse_scores.append(-scores.mean())각 k값에 대해 KNN 회귀 모델을 생성하고 교차 검증을 수행.
교차 검증은 훈련 세트를 여러 부분으로 나누어 모델을 평가하는 과정.
여기서는 3-fold cross-validation을 사용하고, 평균 제곱 오차의 음수 값을 계산하여 mse_scores 리스트에 저장.
그 후 MSE가 가장 낮은 k값을 찾고 이를 출력.
나온 결과값을 시각화하면

적정 k 값을 찾은 후 MSE가 다시 상승하는 것을 볼 수 있다
-> 훈련 데이터와의 과적합으로 인하여 MSE가 다시 증가하는 것
- 과소적합: K값이 증가하면 이웃의 수가 더 많아지기 때문에 모델이 더 단순해지고, 데이터의 복잡한 패턴을 파악하기 어려워진다. 이는 모델이 학습 데이터의 패턴을 충분히 학습하지 못하고, 따라서 학습 데이터에 과소적합되는 경향이 있다. 즉, 모델이 너무 단순하게 설정되어 있어서 새로운 데이터에 대한 일반화 능력이 떨어지는 현상이 발생할 수 있다.
- 이상치에 대한 영향: KNN은 모든 이웃의 거리를 고려하여 예측을 수행하기 때문에 이상치의 영향을 크게 받을 수 있습니다. 이상치가 포함된 데이터에서는 이상치와 가까운 이웃들의 영향으로 인해 예측 결과가 왜곡될 수 있습니다. 따라서 K값을 증가시키면 모델이 더 많은 이웃을 고려하므로 이상치의 영향이 커질 수 있고, 결과적으로 MSE 값이 증가할 수 있습니다.
KNN 분류
load_iris 데이터로 분류 작업 진행
train test로 나눠서 훈련 진행
각 K값에 대해 단순히 테스트 세트의 정확도를 측정하고 시각화

교차 검증을 통해 K값에 따른 모델의 성능을 평가하고 최적의 K값을 찾기

그리드 서치를 수행
훈련 데이터(X_train, y_train)를 사용하여 각 하이퍼파라미터 조합에 대해 교차 검증을 수행하고 최적의 조합을 찾기
최적의 하이퍼 파라미터: {'n_neighbors': 5, 'weights': 'uniform'}
최적의 스토어: 0.980952380952381
이상치 탐지
캘리포니아 주택 데이터셋을 사용하여 이상치를 탐지하는 것은 다소 복잡할 수 있습니다. 일반적으로 이상치는 데이터에서 벗어난 극단적인 값으로 정의되며, 이러한 값은 데이터 분포의 패턴을 깨뜨릴 수 있습니다. 이상치를 탐지하고 처리하는 방법에는 여러 가지가 있습니다. 이상치 탐지를 위한 간단한 방법 중 하나는 박스 플롯(box plot)이나 히스토그램과 같은 시각화 도구를 사용하여 데이터의 분포를 시각적으로 탐색하는 것입니다.
하지만 주어진 데이터셋이 캘리포니아 주택 데이터셋인 경우, 이상치를 직접적으로 확인하기는 어려울 수 있습니다. 일반적으로 이러한 데이터셋은 주택 가격과 관련된 여러 특성을 포함하며, 이러한 특성 간의 관계와 분포를 분석하여 이상치를 식별하는 것이 일반적입니다. 또한 주택 가격 데이터는 종속 변수로 사용되기 때문에 이상치를 식별하고 처리하는 데 특히 주의를 기울여야 합니다.
이상치를 탐지하고 처리하는 방법에는 여러 가지가 있으며, 일반적으로는 다음과 같은 접근 방법이 사용됩니다:
- 시각화를 통한 탐지: 박스 플롯, 히스토그램 등을 사용하여 데이터의 분포를 시각적으로 탐색하고 이상치를 식별합니다.
- 통계적 방법을 활용한 탐지: 평균, 표준편차, 백분위수 등을 사용하여 데이터의 분포를 분석하고 이상치를 식별합니다.
- 기계학습 기법을 활용한 탐지: 이상치 탐지 모델(예: Isolation Forest, One-Class SVM 등)을 사용하여 데이터의 이상치를 식별합니다.
캘리포니아 주택 데이터셋에서 중간 소득(MedInc) 특성을 사용하여 KNN을 이용하여 이상치를 탐지
거리 기준으로 이상치 점수 계산
이상치 점수가 특정 기준을 넘으면 이상치로 판단
여기선 상위 5%를 이상치로 간주
시각화
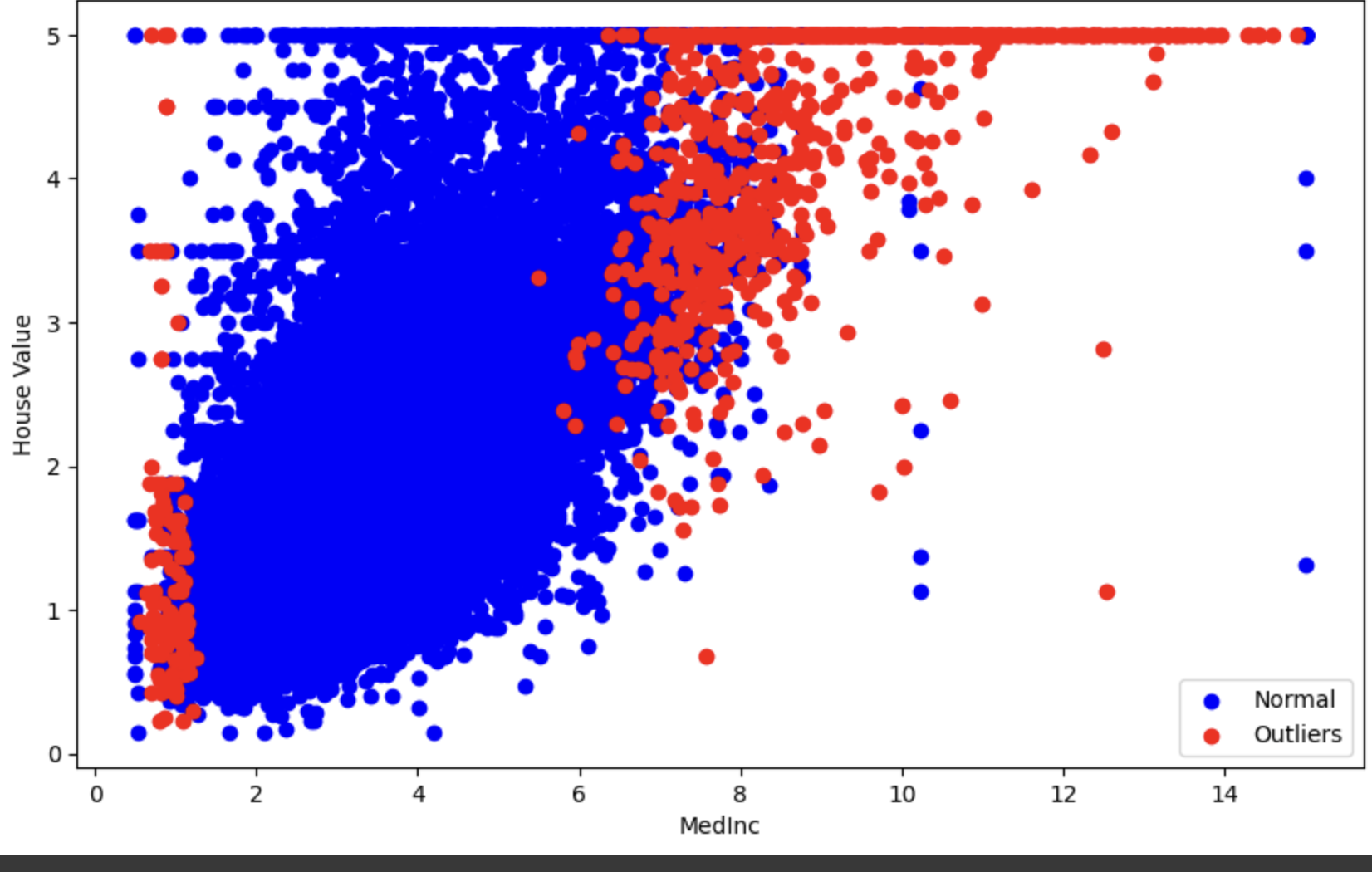
그래프를 보면 중위 소득이 대부분 2-8 사이 분포하고 있고, 그때의 주택 가격은 0-5까지 고르게 분포하고 있는 것을 볼 수 있다.
이상치에 경우 중위소득 1과 8-14 사이에 분포하고 있다. 특히 주택가격이 높은 곳일수록 이상치가 많이 분포하고 있는 걸을 알 수 있다.
소득이 클수록 집값 또한 등가하는 것을 알 수 있다.
'공부 > 머신러닝' 카테고리의 다른 글
| 선형회귀분석(Linear_regression) (2) | 2024.05.25 |
|---|---|
| 회귀분석 개념 공부 (0) | 2024.05.19 |
| 임계점평가지표 (1) | 2024.03.31 |
| 머신러닝, 평가지표 (2) | 2024.03.24 |
| 교차검증, (k-fold cross validation) (1) | 2024.03.24 |




