고정 헤더 영역
상세 컨텐츠
본문
안녕하십니까 공부가 싫은 남자 공싫남입니다
오늘은 회귀분석 기초 개념에 대해 공부해보겠습니다
먼저 변수에 종류에 대해 알아보면
- 원인 (조작·제어)
- 독립변수 (Independent variable): 실험이나 연구에서 조작하거나 제어할 수 있는 변수. 결과에 영향을 미치는 원인으로 간주됩니다.
- 설명변수 (Explanatory variable): 독립변수와 비슷한 의미로, 결과를 설명하는 변수입니다.
- 예측변수 (Predictor variable): 미래의 결과를 예측하는 데 사용되는 변수입니다.
- 위험인자 (Risk factor): 특정 결과에 영향을 줄 수 있는 위험 요소로 간주되는 변수입니다.
- 공변량 (Covariate): 연속형 자료로, 독립변수와 함께 분석에 포함되는 변수입니다.
- 요인 (Factor): 범주형 자료로, 실험에서 수준별로 나뉘는 변수입니다.
- 결과 (측정한 결과)
- 종속변수 (Dependent variable): 독립변수에 의해 영향을 받는 결과 변수입니다.
- 반응변수 (Response variable): 실험에서 반응을 측정하는 변수입니다.
- 결과변수 (Outcome variable): 연구나 실험의 결과로 나타나는 변수입니다.
- 표적변수 (Target variable): 예측 모델에서 예측하고자 하는 변수입니다.
라고 합니다.
회귀 분석 모델

회귀 분석의 기본적인 모델 형태이다.
X가 일차인 선형회귀모델로, 독립변수 X가 종속변수 Y에 미치는 영향을 추정하는 데 사용된다.
와 β1는 회귀 계수로, 데이터를 통해 추정되고, ϵi는 실제 관측값이 모델의 예측값과 얼마나 다른지를 나타내는 오차이다.
궁극적으로 ϵi 값을 최소화하는 것이 목표라고 할 수 있다.
변수 간 선형 관계
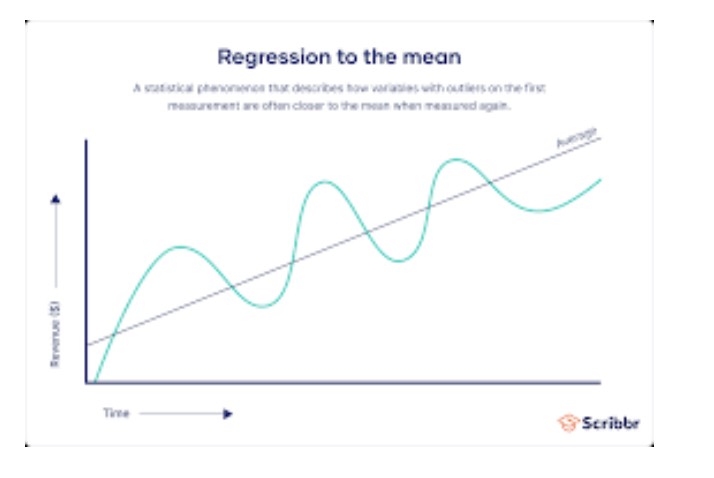
평균으로의 회귀 (Regression to the mean)
'평균으로의 회귀'는 통계적 현상으로, 처음 측정에서 극단값을 보이는 변수들이 다시 측정될 때 평균에 더 가까운 값을 보이는 경향 말한다
그래프를 보면 시간이 지남에 따라 초기에 컸던 변동성이 갈수록 줄어드는 것을 볼 수 있다.
여기서 직선은 평균값으로의 회귀 경향을 보여주는 직선이다.
실제 데이터의 변동은 곡선으로 나타나지만, 전반적인 경향은 평균으로 수렴한다.

두 변수 사이의 관계를 나타낸 그래프이다
직선은 데이터 점들을 최적으로 설명하는 직선이다.
한 변수가 증가할 때 다른 한 변수가 증가하는 양의 상관관계를 나타내고 있다.
선형회귀 기본 가정
선형성 (Linearity)
- 설명: 설명변수 X와 반응변수 Y 사이에 존재하는 관계는 선형이어야 합니다. 주어진 X의 값에서 Y의 기대값은 E(Y∣X=x)=B0+B1x의 형태로 표현됩니다.
- 확인 방법: 선형 관계가 지속적인지 확인하기 위해 산점도나 잔차 예측값을 통해 시각적으로 확인합니다.
독립성 (Independence)
- 설명: 오차항은 서로 독립적이어야 합니다. 즉, 한 오차항이 다른 오차항에 영향을 주지 않아야 합니다.
- 확인 방법: 시간의 순서에 따라 Durbin-Watson 통계량을 계산하여 오차항의 독립성을 검사합니다. Durbin-Watson 값이 0에 가까우면 양의 자기상관, 4에 가까우면 음의 자기상관을 나타내며, 일반적으로 1.5에서 2.5 사이의 값이면 독립성을 만족한다고 봅니다.
등분산성 (Homoscedasticity)
- 설명: 모든 독립변수의 값에 대한 오차의 분산이 일정해야 합니다. 독립변수의 크기에 상관없이 일관된 변동을 보여야 합니다.
- 확인 방법: 잔차 대 적합값 플롯을 사용하여 등분산성을 평가합니다. 플롯에서 패턴이 보이거나 퍼짐 변화가 있으면 이 가정이 위반된 것입니다.
정규성 (Normality)
- 설명: 오차항은 정규 분포를 따라야 합니다. 특히 큰 표본에서 이 가정이 중요합니다. 정규 분포를 따르지 않으면 회귀 분석의 통계적 검정 결과가 부정확할 수 있습니다.
- 확인 방법: Q-Q 플롯, 정규성 검정 (Kolmogorov-Smirnov, Shapiro-Wilk 테스트 등)을 사용하여 오차항의 분포가 정규 분포를 따르는지 확인합니다.
이 가정들이 충족되지 않으면 회귀 모델의 예측력과 해석력이 떨어질 수 있습니다. 따라서 위의 가정들을 충족시키는 모델을 만들기 위하여 노력해야합니다.
선형 회귀 그래프 알아보기
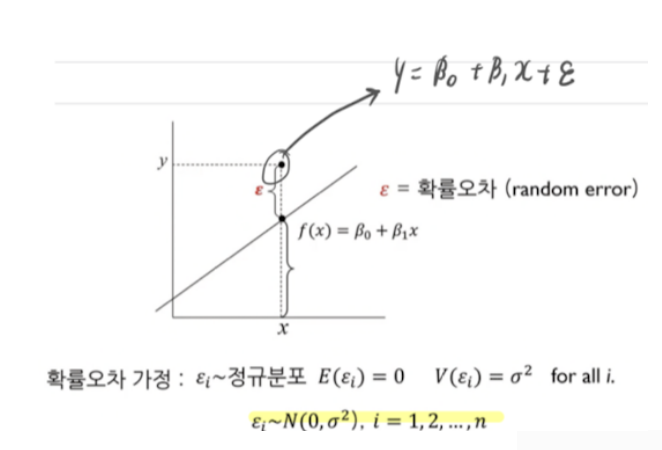
- 모델: Y=β0+β1X+ϵ
- 오차항 (ϵ): 실제 관측값과 회귀 모델에 의해 예측된 값 사이의 차이를 나타냅니다. 이 차이를 확률 오차(random error)라고 합니다.
- 수식: 오차항은 정규 분포를 따른다는 가정입니다. ϵi∼N(0,σ2) 여기서 ϵi는 평균이 0이고 분산이 σ^2인 정규 분포를 따른다고 가정합니다.
- 기대값 : 0
- 분산 : σ^2
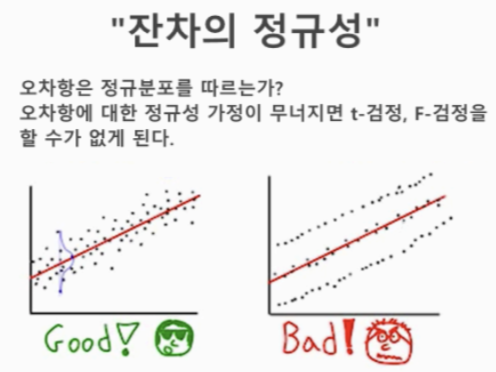
오차항이 정규분포를 따르지 않는 오른쪽 그래프에 경우 t-검정, F-검정을 진행할 수 없다.
최소제곱법
- 목적: 주어진 데이터 (xi,yi)에 대해 선형 회귀 직선 y=ax+b를 구하는 것입니다. 이 때 각 데이터 점과 회귀 직선 사이의 오차(잔차)의 제곱합을 최소화합니다.

정규 방정식 XT(Y−X )=0
여기서 X는 절편을 포함한 예측 변수의 행렬, Y는 결과의 벡터, 는 계수의 벡터를 나타냅니다.
이 방정식은 선형 회귀 분석에서 계수를 추정하는 데 사용됩니다.
정규 방정식(Normal Equation)은 선형 회귀 모델에서 최적의 계수를 찾는 방법 중 하나입니다. 선형 회귀의 목표는 주어진 데이터에 가장 잘 맞는 직선(혹은 초평면)을 찾는 것인데, 정규 방정식은 이를 수학적으로 해결하는 방법을 제공합니다.
정규 방정식의 유도
선형 회귀 모델은 일반적으로 다음과 같은 형태를 가집니다:
Y=Xβ+ϵ
여기서 Y는 응답 변수 벡터, 는 설계 행렬(데이터 포인트의 특징을 포함하며, 각 행은 하나의 데이터 포인트, 각 열은 하나의 특징을 나타냄), β는 계수 벡터, 은 오차 항입니다.
최소제곱법은 오차의 제곱 합, 즉 (Y−Xβ)T(Y−Xβ)을 최소화하는 를 찾는 방법입니다. 이 값을 로 미분하고 0으로 설정하면 다음과 같은 정규 방정식을 얻을 수 있습니다:
XT(Y−Xβ)=0
위 식을 풀면 계수에 대한 해를 얻을 수 있습니다:
β=(XTX)−1XTY
정규 방정식의 특징 및 한계
- 해석적 해: 정규 방정식은 해석적으로 계수를 직접 계산합니다. 즉, 반복적인 접근 방식 없이 닫힌 형태의 해를 제공합니다.
- 계산 복잡성: XTX의 역행렬을 계산하는 것은 계산적으로 비용이 많이 들 수 있습니다. 특히 변수의 수가 많을 때, 이 행렬은 매우 크고 계산하기 어려울 수 있습니다.
- 조건의 좋지 않은 문제: XTX가 역행렬을 가지지 않거나 역행렬을 계산하기 어려울 경우(예: 특이 행렬 또는 불안정한 수치 조건) 정규 방정식은 사용하기 적합하지 않을 수 있습니다. 이러한 경우, 최소제곱 문제를 해결하기 위해 수치적으로 안정된 다른 방법(예: QR 분해, 경사 하강법)을 사용할 수 있습니다.
결정 계수는 회귀 모델의 설명력을 측정하는 지표로 사용되며, 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타냅니다.
R^2 값은 0과 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 잘 설명하고 있다는 의미입니다.


다중공선성
회귀 모델에서 두 개 이상의 예측 변수가 서로 상관 관계가 높을 때 발생하는 문제로, 이는 회귀 분석의 정확성과 신뢰성을 저하시킬 수 있습니다.
다중공선성의 문제점
- 계수 추정의 불안정성: 다중공선성이 있는 경우, 작은 데이터의 변동에도 계수(가중치)가 크게 변할 수 있습니다.
- 계수 해석의 어려움: 높은 상관관계를 가진 변수들 때문에 어느 변수가 결과에 더 중요한 영향을 미치는지 해석하기 어려워집니다.
- 통계적 유의성 감소: 다중공선성이 있는 변수들은 통계적으로 유의미한 결과를 얻기 어려워지는 경우가 많습니다.
다중공선성의 진단 방법
- 상관 행렬(Correlation Matrix): 변수들 간의 상관계수를 확인하여, 높은 상관관계를 보이는 변수 쌍을 식별합니다.
- 분산 팽창 요인(Variance Inflation Factor, VIF): VIF가 5 이상이면, 해당 변수는 다른 변수들과의 높은 상관관계를 가지고 있음을 의미합니다. 일반적으로 VIF가 10 이상일 때 다중공선성이 심각하다고 판단됩니다.
다중공선성 해결 방법
- 변수 제거: 높은 다중공선성을 보이는 변수 중 하나를 제거하여 모델에서 제외합니다.
- 주성분 분석(PCA): 주성분 분석을 통해 변수들을 새로운 선형 조합으로 변환하여, 다중공선성의 영향을 줄이면서도 정보를 유지합니다.
- 정규화 기법 사용: 릿지(Ridge) 회귀, 라쏘(Lasso) 회귀와 같은 정규화 기법을 사용하여 다중공선성의 영향을 감소시킵니다.
'공부 > 머신러닝' 카테고리의 다른 글
| 선형회귀분석(Linear_regression) (2) | 2024.05.25 |
|---|---|
| ML1, KNN 알고리즘기반 (0) | 2024.05.05 |
| 임계점평가지표 (1) | 2024.03.31 |
| 머신러닝, 평가지표 (2) | 2024.03.24 |
| 교차검증, (k-fold cross validation) (2) | 2024.03.24 |




