고정 헤더 영역
상세 컨텐츠
본문
이어서 진행한다.
2.3 Optimality Conditions
우리는 이제 선형 프로그래밍의 강한 이중성 정리(Strong Duality Theorem)에 대해 알아보고자 한다. 이 정리는 원 문제(primal problem)와 이중 문제(dual problem) 사이의 최적해 관계를 규명한다.
강한 이중성 정리
간단히 말해 강한 이중성 정리는 원 문제와 이중 문제가 모두 실행 가능한 해를 가질 경우, 두 문제의 최적해의 목표 함수 값이 같다고 말한다. 즉, 원 문제의 최적해 와 이중 문제의 최적해 에 대해서 c^Tx=b^Ty가 성립한다.
최적성 조건
는 원 문제의 최적해로서 다음 조건을 만족해야 한다:
- 실행 가능성(Primal feasibility): 및 x≥0
- 이중 실행 가능성(Dual feasibility): A^Ty≤c
- 이중 갭 없음(No duality gap): c^Tx=b^Ty
보완 느슨함(Complementary Slackness)
- 보완 느슨함은 최적해 조건을 더욱 명확히 하는 개념으로, 각 변수에 대해 xi(si)=0이 성립해야 한다. 여기서s=c−ATy는 이중 슬랙(dual slack) 변수로, 원 문제의 제약과 이중 문제의 제약 사이의 차이를 나타낸다.
- 이 조건은 xi>0인 경우에 해당하는 에 대해서는 가 0이어야 하며(즉, 이중 문제의 해당 제약이 타이트하게 결합), 인 경우 xi는 0이어야 함을 의미한다.
이전 포스팅의 약한 이중성과 위의 강한 이중성, 보안 느슨함에 대해서는 추후 더 자세히 다루려고 한다.
개인적으로 매우 중요한 개녕이라고 생각해 증명까지 해보려고 한다.
최적해의 식별
이러한 조건들은 선형 프로그래밍 문제를 해결할 때, 원 문제와 이중 문제 각각에 대한 최적해가 서로 어떻게 연관되어 있는지를 정확히 파악하는 데 중요하다. 원 문제의 어떤 해와 이중 문제의 해가 이 조건들을 만족시키면, 그 해들은 각각의 문제에 대한 최적해임이 보장된다. 이는 원 문제와 이중 문제가 서로 강하게 연결되어 있음을 보여주며, 한 문제의 해를 통해 다른 문제의 해를 유추할 수 있는 근거를 제공한다.
2.4 The Simplex Method
LP를 푸는 방법 중 가장 잘 알려진 방법 중 하나가 simplex method이다. 이 방법을 소개하기 위해 한 가지 예시를 들겠다.
이 문제는 선형 프로그래밍을 이용한 간단한 채권 포트폴리오 선택 문제를 다루고 있다. 주어진 예시에서는 포트폴리오 매니저가 100,000달러를 두 가지 유형의 채권에 배분하려고 한다. 이는 각각 기업 채권과 정부 채권으로, 각 채권의 수익률, 만기 기간 및 평가 등급이 제공된다. 문제의 목표는 이러한 자금을 최적으로 배분하여 포트폴리오의 수익률을 최대화하는 것이다.
문제 설명:
- 기업 채권: 4% 수익률, 3년 만기, Moody's 등급 A (수치 2)
- 정부 채권: 3% 수익률, 4년 만기, Moody's 최고 등급 Aaa (수치 1)
포트폴리오 매니저는 다음과 같은 조건을 만족하면서 투자해야 한다:
- 포트폴리오의 평균 등급이 Aa (수치적 등가 1.5) 이하이어야 하며,
- 포트폴리오의 평균 만기가 3.6년을 초과하지 않아야 한다.
선형 프로그래밍 모델:
목적 함수:

슬랙 변수 x3, , 는 각 제약 조건이 등호로 만족되는 경우에 필요한 값들을 보정하기 위해 사용된다.
2.4.1 Basic Solutions
선형 프로그래밍의 표준 형식
선형 프로그래밍 문제는 일반적으로 다음과 같이 표현됩니다:
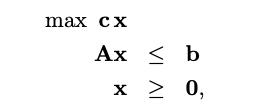

슬랙 변수와 기본 해
- 슬랙 변수 는 원래 문제의 부등식 제약을 등식 제약으로 변환하기 위해 추가된다.
- 이를 통해 확장된 문제는 [A,I][x,xs]=b의 형태를 가지며, 여기서 I는 단위 행렬이다.
- 기본 해: 변수 벡터를 와 xs로 분할하고, 비기본(nonbasic) 변수를 0으로 설정하여 해를 구한다.
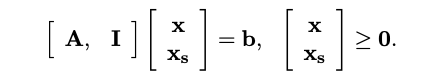
개념 설명
B 행렬은 선택된 기본 변수에 해당하는 계수 행렬 A의 부분 행렬이다. 이 행렬은 행렬 에서 독립적인 열들을 기반으로 구성되며, 이 경우에는 슬랙 변수를 포함한 확장된 계수 행렬 에서 선택된다.
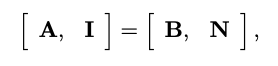
기본 변수 와 비기본 변수 로 변수 집합을 나눈다. 기본 변수는 해를 구성하는 데 사용되며, 비기본 변수는 0으로 설정된다.
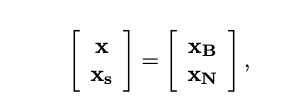
계산 과정
위의 식을 바탕으로 재구성한 식
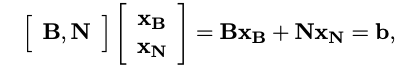
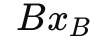
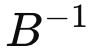

: 이 식은 B의 역행렬과 상수 벡터 의 곱으로, 기본 변수들의 값을 직접 계산한다.


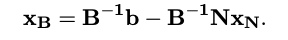
2. 기본 해 설정:
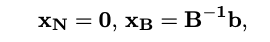
3. 목적 함수 계산:

2x2 행렬 가 다음과 같이 주어졌다고 가정하자:

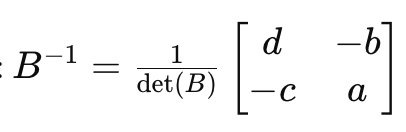
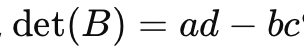
'공부 > 최적화' 카테고리의 다른 글
| Optimization Methods in Finance Chapter 8.1.2-8.1.3 (0) | 2025.01.14 |
|---|---|
| Optimization Methods in Finance Chapter 8.1 (2) | 2025.01.13 |
| Optimization Methods in Finance Chapter 3.1-3.2 (3) | 2024.11.11 |
| Optimization Methods in Finance Chapter 2.1-2.2 (0) | 2024.11.05 |
| Optimization Methods in Finance Chapter 1.3 (8) | 2024.10.29 |




