Optimization Methods in Finance Chapter 8.1

8.1 Mean-Variance Optimization

 

이번 장은Markowitz의 평균-분산 최적화(mean-variance optimization, MVO)에 대해 다루고 있다.

이는 포트폴리오 관리에서 기대수익과 위험(분산)을 적절히 조합하여 최적의 자산 배분을 찾는 수학적 방법이다.

 

MVO의 핵심 아이디어

• 기대수익을 최대화하거나 위험(분산)을 최소화하면서 최적의 투자 비율을 찾는 것을 목표로 한다.
• 수학적 표현:

 

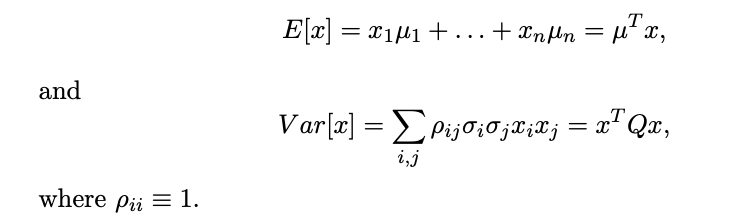
여기서 μ는 자산들의 기대수익을 나타내는 벡터이고, x는 각 자산에 투자된 비율이다.

또한 Q는 자산 간의 공분산 행렬이다.

 

효율적 프론티어(efficient frontier)

• 효율적 포트폴리오: 같은 위험 수준에서 기대수익이 가장 높은 포트폴리오, 또는 같은 기대수익에서 위험이 가장 낮은 포트폴리오.
• 효율적 포트폴리오들을 그래프로 그리면 "효율적 프론티어"라는 곡선이 나타난다. 투자자는 이 곡선 상에 있는 포트폴리오를 선택하는 것이 합리적이다.

 

제약 조건

MVO에서 고려하는 제약 조건:

1. 모든 자산에 투자된 비율의 합은 100%여야 한다 (∑xi​=1).
2. 투자자의 선호에 따라 특정 자산에 대한 최소/최대 투자 비율을 설정할 수 있다.
3. 기대수익이 특정 수준 이상이거나, 위험이 특정 수준 이하가 되도록 요구할 수 있다.

 

최적화 문제로 표현

이 문제는 이차계획법(Quadratic Programming)으로 풀린다:

 

• 목적 함수: 포트폴리오의 분산을 최소화하는 것 (x^TQx).
• 제약 조건:
  • μ^Tx≥R: 기대수익이 R 이상이 되어야 한다.
  • Ax=b: 투자 비율의 합은 1.
  • Cx≥d: 추가적인 투자 조건.

 

8.1.1 Example

예시를 하나 살펴보자.

해당 데이터는 1960년부터 2003년까지의 총 수익률(Total Return)을 나타낸 것이다.

왼쪽부터 미국 주식, 채권, 현금(금리)를 나타내었다.

이것을 포함한 포트폴리오에 MVO를 적용해보자.

 

먼저 아래 식을 사용하여 수익률을 계산해보자.

여기서 Ii,t​는 t년의 특정 자산 i의 총 수익률

 

그 다음 평균 수익률을 계산한다.

(산술평균)

해당 식을 사용해서 계산해보면,

위의 표와 같이 나오는 것을 알 수 있다.

(기하평균)

장기 수익률에 적합한 기하평균으로 도출된 값을 사용

 

그 후 포트폴리오의 위험(분산)을 계산하기 위한 공분산 행렬 사용

 

공분산(Covariance)

• 공분산은 두 변수 간의 상호 관계를 측정한다.
  • 양수: 두 변수가 같은 방향으로 움직임 (예: 둘 다 상승).
  • 음수: 두 변수는 반대 방향으로 움직임 (하나는 상승, 다른 하나는 하락).
  • 0: 두 변수 간에 상관관계가 거의 없음.

공분산 행렬을 사용하는 이유는?

상관관계가 낮은 자산을 섞으면 포트폴리오 전체의 위험을 줄일 수 있다(분산 투자 효과).

 

(공분산 행렬 예시)

 

• 주식과 채권의 상관계수: 0.2199 → 약한 양의 상관관계.
• 채권과 현금의 상관계수: −0.0545 → 거의 무관.
  
  

이를 바탕으로 최적화 문제 설정

결과를 살펴보면

표에서는 수익률 R이 6.5%에서 10.5%까지 변화할 때, 각 자산의 최적 투자 비율을 보여준다.

 

위의 그래프는 효율적 프론티어(Efficient Frontier)와 효율적 포트폴리오의 구성을 나타낸다.

 

좌측 그래프는 효율적 프론티어를 나타낸다.

 

• X축 (Standard Deviation %): 포트폴리오의 위험(변동성)을 나타냅니다. 변동성은 포트폴리오의 수익률이 얼마나 변동하는지를 보여준다.
  • 낮을수록 안정적인 투자.
  • 높을수록 더 높은 위험을 감수.
• Y축 (Expected Return %): 포트폴리오의 기대수익률을 나타낸다.
  • 높을수록 더 많은 수익을 기대할 수 있음.

 

 

위험(표준편차)이 증가할수록 기대수익률도 증가한다

 

오른쪽 그래프는 효율적 포트폴리오의 자산 구성을 나타낸다.

 

• X축 (Expected Return %): 포트폴리오의 기대수익률.
  • 6.5%에서 10.5%까지의 기대수익률 범위에서 효율적 포트폴리오의 구성을 보여준다.
• Y축 (Percent invested in different asset classes): 각 자산에 투자된 비율(%)을 나타낸다.
  • 검정: 주식(Stocks)
  • 회색: 채권(Bonds)
  • 흰색: 현금(MM)
• 낮은 기대수익률은 안정적인 자산(현금, 채권)에 집중.
• 높은 기대수익률은 위험이 높은 자산(주식)에 집중.

결론

해당 예제는 이론을 실제 데이터에 적용하여 주식, 채권, 현금의 조합으로 최적의 포트폴리오를 찾는 과정을 보여줍니다. 이를 통해 투자자는 위험과 수익 간의 균형을 유지하면서 최적의 투자 전략을 설계할 수 있습니다.