고정 헤더 영역
상세 컨텐츠
본문
8.1.2 Large-Scale Portfolio Optimization
- 대규모 문제(Large-Scale Method)란?
- 수백 개, 혹은 수천 개의 자산으로 구성된 포트폴리오를 최적화하는 상황을 말한다.
- 각 자산의 기대수익률(µ)과 공분산 행렬(Q)을 활용하여 포트폴리오를 구성한다.
- 문제점:
- 마코위츠 모델은 자산 간의 분산 투자를 보장하지 않는다.
- 특정 자산(소형주, 특정 섹터 등)에 과도한 투자 비중을 할당하거나 비합리적인 공매도(short position)를 발생시킬 수 있다.
해결 방안
(1) 분산 투자 제약 (Diversification Constraints)
- 분산 투자를 보장하기 위해 제약 조건을 추가한다.
- 각 자산 xi의 투자 비율이 일정 한도 을 초과하지 않도록 설정한다.
(2) 거래 비용 제약 (Transaction Costs Constraints)
- 기존 포트폴리오(x0)와 새로운 포트폴리오() 간의 변화가 너무 크지 않도록 제한한다.
(3) 파라미터 추정 (Parameter Estimation)
- 마코위츠 모델은 자산의 기대수익률(µ)과 공분산(σ)을 정확히 추정해야만 최적 포트폴리오를 도출한다.
마코위츠 모델의 약점
- 데이터 민감성:
- 기대수익률(µ) 또는 공분산(σ)의 작은 변화가 포트폴리오 최적화 결과를 크게 바꿀 수 있다.
- 해결책:
- 여러 방법(CAMP, 샘플링)을 사용해 평균 µ와 공분산 σ를 추정.
- 여러 결과를 결합하여 보다 안정적인 포트폴리오를 생성.
정리
실질적인 제약 조건(분산 투자, 거래 비용, 파라미터 추정 등)을 추가하여 대규모 포트폴리오를 효과적으로 최적화하는 방법을 설명한다.
최적 포트폴리오를 설계할 때 데이터의 민감성을 줄이고, 보다 신뢰할 수 있는 결과를 얻기 위해 다양한 접근이 필요합니다.
8.1.3 The Black-Litterman Model
Black-Litterman 모델은 시장 균형(market equilibrium)과 투자자의 주관적 의견을 결합하여 포트폴리오의 기대수익률(μ)을 계산하는 방법이다. 이 모델은 마코위츠의 평균-분산 이론(MVO)의 문제점을 보완하기 위해 고안되었다.
1. Black-Litterman 모델의 구성
(1) 시장 균형 (Market Equilibrium)
- 시장 균형에서의 기대수익률 :
- 는 모든 투자자가 동일한 정보를 가진다고 가정할 때의 기대수익률.
- , 여기서 는 공분산 행렬, 은 시장 포트폴리오의 비중.
(2) 투자자의 의견 (Investor Views)
- 투자자는 시장 균형 외에도 자산의 미래 성과에 대한 자신의 의견(views)을 가질 수 있다.
- 투자자의 의견은 다음과 같이 표현된다:
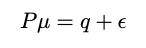
- : 행렬로, 투자자의 의견이 적용되는 자산을 나타냄.
- q: 투자자의 의견 벡터 (예: 특정 자산이 2% 더 나을 것이라는 예측).
- : 정규분포를 따르는 오차항 (투자자의 의견에 대한 불확실성).
(3) 최종 결합 기대수익률
- 시장 균형 π와 투자자의 의견 q를 결합하여 최종 기대수익률 μˉμˉμˉ를 계산한다:
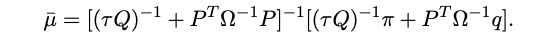
2. 모델 적용 예시
8.1.1에서 우리는 미국의 주식, 채권, 현금의 수익률을 계산했다.

주식, 채권, 현금의 시장 균형 수익률은 위의 표와 같다.
여기에 투자자의 두 가지 의견도 존재한다.
- 현금(Money Market)이 내년에 2% 상승할 것 → 강한 신뢰 ().
- S&P 500(주식)이 10년 만기 국채(채권)보다 5% 더 나을 것 → 약한 신뢰 ().
이것은 행렬로 표현할 수 있다.

이 두가지 요소를결합하여 위의 공식에 대입하면 μˉ를 구할 수 있다.

3. 효율적 프론티어의 변화
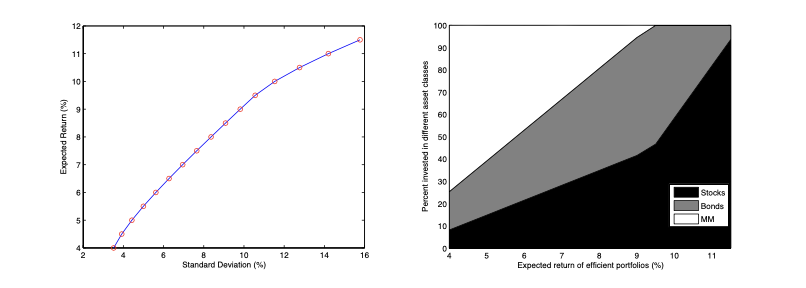
- Black-Litterman 접근법으로 효율적 프론티어와 포트폴리오 구성이 변한다.
- 결과적으로 투자자의 의견을 반영한 새로운 효율적 포트폴리오가 생성된다:
- 낮은 위험에서는 채권과 현금 비중이 높음.
- 높은 위험에서는 주식 비중이 높음.
4. Black-Litterman 모델의 강점
- 시장 균형과 투자자의 의견 결합:
- 투자자의 의견을 모델에 포함하면서 시장 데이터를 보완.
- 불확실성 반영:
- 투자자의 신뢰도를 공분산 행렬 로 조정.
- 안정성:
- 마코위츠 모델보다 덜 민감하여 데이터 변화에 더 안정적.
Use the KKT conditions to prove the above equation.
Black-Litterman 모델에서 최종 기대수익률 를 도출하는 과정과 이를 KKT(Karush-Kuhn-Tucker) 조건으로 증명하는 방법에 대해 알아보자.
1. 투자자의 100% 신뢰와 일반적인 경우
(1) 100% 신뢰 (Special Case of 100% Confidence)
- 투자자가 자신의 의견(view)에 대해 100% 신뢰를 가진 경우:
- 의견이 시장 균형에서의 기대수익률(π)을 완전히 대체한다.
- 따라서 , 즉 투자자의 의견만 반영된다.
(2) 일반적인 경우 (Partial Confidence)
- 투자자가 자신의 의견에 대해 100% 신뢰하지 않을 때:
- 의견 은 시장 균형 기대수익률(π)과 함께 결합된다.
- 결합은 투자자의 신뢰도(Confidence)와 시장 데이터의 신뢰도(Precision)에 따라 가중된다.
이에 대한 식은 앞에서도 언급했듯 아래와 같다.
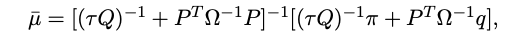
3. KKT 조건을 통한 증명
- 는 위 수식에서 최적화 문제를 통해 계산된다.
- 최적화 문제는 다음과 같다:
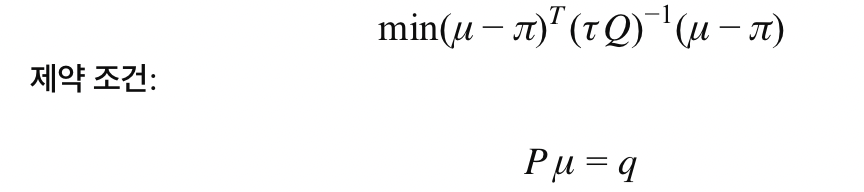
(1) KKT 조건이란?
- KKT 조건은 제약이 있는 최적화 문제에서 최적해를 찾기 위한 필요충분 조건이다.
- 위 문제에 대해 KKT 조건은 다음과 같이 적용된다:
- Lagrangian 정의:

여기서 는 Lagrange 승수.
- 최적 조건:
- : 목적 함수의 미분이 0이어야 함.
- 제약 조건 를 만족해야 함.
(2) 증명
- 위 조건을 활용하면 최적 기대수익률 μˉ가 도출된다:
'공부 > 최적화' 카테고리의 다른 글
| Optimization Methods in Finance Chapter 8.2 (0) | 2025.01.14 |
|---|---|
| Optimization Methods in Finance Chapter 8.1.4 (0) | 2025.01.14 |
| Optimization Methods in Finance Chapter 8.1 (2) | 2025.01.13 |
| Optimization Methods in Finance Chapter 3.1-3.2 (3) | 2024.11.11 |
| Optimization Methods in Finance Chapter 2.3-2.4 (1) | 2024.11.05 |




